Dưới trên đây là toán hình 9 nâng cao mới nhất tổng thích hợp những bài toán nâng cấp lớp 9 học tập kì 1 giúp những bận khối hệ thống lại kiến thức cũng giống như dạng toán nâng cấp và các chuyên de hình học tập 9 . Hãy thuộc theo dõi bên dưới với trungvietlaptop.com nhé.
Bạn đang xem: Toán nâng cao lớp 9 hình học
Video lý giải làm toán 9 nâng cấp hình học
Tổng đúng theo những vấn đề hình 9 nâng cao
Để học tốt môn Toán lớp 9, ở kề bên các bài Giải bài xích tập Toán 9, loạt bài bác Chuyên đề Toán 9 có hai phần: siêng đề Đại số 9 và siêng đề Hình học 9 được biên soạn bám quá sát theo nội dung chương trình học tập Toán lớp 9 gồm: Lý thuyết, bài xích tập từ luận, bài tập trắc nghiệm tương ứng với mỗi chuyên đề.
Chuyên đề: Hệ thức lượng trong tam giác vuông
A. Cách thức giải
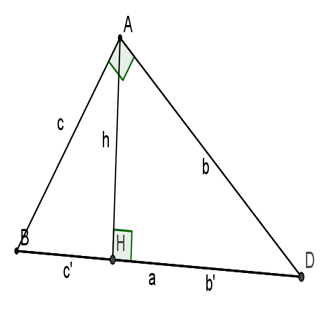
Cho tam giác ABC vuông góc trên A, đường cao AH. Khi ấy ta có:
1, c2 = ac’, b2 = ab’
2, a2 = b2 + c2
3, ah = bc
4, h2 = b’.c’
5, 1/h2 = 1/b2 + 1/c2
B. Bài bác tập trường đoản cú luận
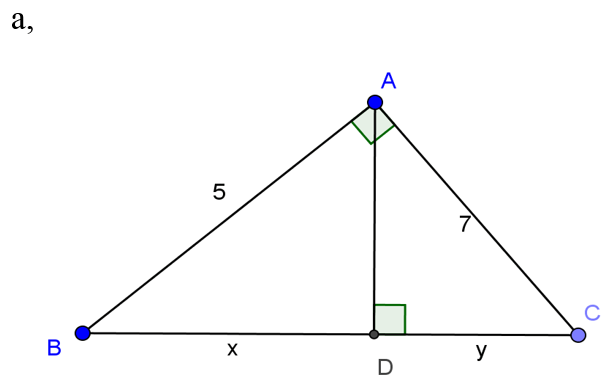
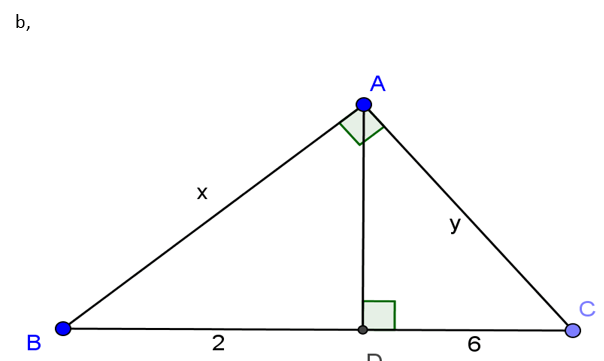
Bài 1: Tính x, y trong số trường phù hợp sau
Hướng dẫn giải
a, Áp dụng định lý py-ta-go vào tam giác vuông ABC có:
BC2= AB2+ AC2
BC2= 52+ 72
BC2= 74
Suy ra BC = √74
Áp dụng hệ thức lượng vào tam giac vuông ABC: AB2 = BD.BC
=> BD = AB2/BC => x = 25/√74
DC = BC – BD = √74 – 25/√74 = 49/√74
Vậy x = 25/√74 và y = 49/√74
b) Ta có: BC= BD + DC = 2 + 6 = 8
Áp dụng hệ thức lượng ta có:
AB2= BD.BC = 2.8 = 16. Suy ra AB = 4 tốt x = 4.
AC2= DC.BC = 6.8 = 48. Suy ra AC = √48 hay y = √48
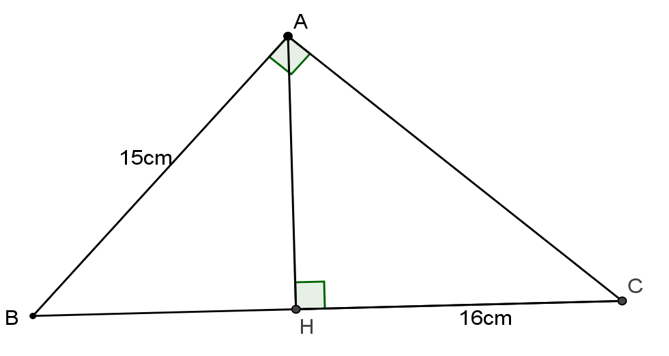
Bài 2: Cho tam giác ABC vuông tại A, mặt đường cao AH. Tính BC, AC, AH biết AB = 15cm, HC = 16cm.
Hướng dẫn giải
Áp dụng hệ thức lượng trong tam giác vuông ABC có:
AC2 = CH.BC = 16.BC
AB2 + AC2 = BC2
⇔ 152 + 16.BC = BC2
⇔ BC2 – 16.BC – 225 = 0
⇔ BC2 – 25BC + 9BC – 225 = 0
⇔ BC(BC – 25) + 9(BC – 25) = 0
⇔ (BC – 25)(BC + 9) = 0
⇔ BC = 25 hoặc BC = -9(loại)
=> AC2 = 16.BC = 16.25 = 400
=> AC = 20
+ Xét tam giác vuông ABC có: AH.BC = AB.AC (hệ thức lượng)
Vậy BC=25(cm); AC=20(cm); AH=12(cm)
Bài 3: Cho tam giác ABC tất cả AB = 48cm, BC = 50cm, AC = 14cm. Tính độ nhiều năm phân giác giác góc C
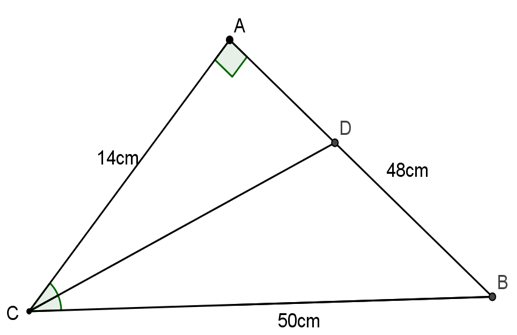
Hướng dẫn giải
Xét tam giác ABC, ta có
BC2 = 502 = 2500
AB2 + AC2 = 142 + 482 = 2500
=> BC2 = AB2 + AC2
=> Tam giác ABC vuông tại A
Có DA/DB = CA/CB = 14/50 = 7/25 (tính hóa học tia phân giác)
=> DB = 25/7 DA.
Ta tất cả DA + DB = AB
⇔ da + 25/7 domain authority = AB ⇔ DA. 32/7 = 48 ⇔ da = 10,5cm
Xét tam giác vuông ACD, theo đinh lí Pi-ta-go ta có
CD2 = AC2 + AD2 = 142 + 10,52 = 306,25 => CD = 17,5cm
Bài 4: Cho tam giác ABC vuông trên A, AB=24cm, AC=32cm. Đường trung trực của BC cắt AC, BC theo đồ vật tự D và E. Tính DE.
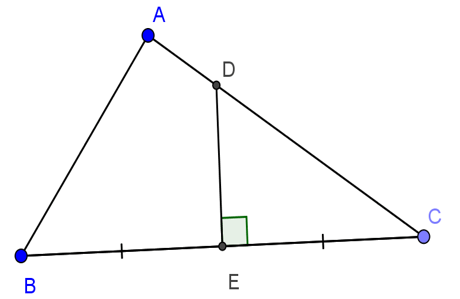
Hướng dẫn giải
Xét tam giác vuông ABC, ta có:
BC2 = AB2+ AC2 ( theo định lý py-ta-go)
BC2 = 242+ 322
BC2 = 1600
BC = 40(cm)
EC = BC : 2 = 40 : 2 = 20(cm)
Xét tam giác vuông ngân hàng á châu acb và tam giác vuông ECD có:
Có ∠A = ∠E = 90o
∠C chung
=> Tam giác ngân hàng á châu acb ∾ tam giác ECD (g.g)
=> AC/EC = AB/ED
=> ED = AB.EC/AC = 15cm
Vậy ED = 15cm
Chuyên đề: Đường tròn
A. Phương thức giải
1, Định nghĩa con đường tròn
Đường tròn là quỹ tích những điểm giải pháp đều một điểm thắt chặt và cố định trong khía cạnh phẳng.
Qua ba điểm không thẳng hàng, ta vẽ được một và có một đường tròn.
Chú ý:
– ko vẽ được đường tròn nào đi qua ba điểm thẳng hàng.
– Nếu hai tuyến phố tròn bao gồm 3 điểm bình thường thì chúng nên trùng nhau
– Để khẳng định một đường tròn ta khẳng định tâm và nửa đường kính của nó hoặc 3 điểm riêng biệt thuộc con đường tròn.
– Để minh chứng nhiều điểm vị trí một đường tròn ta chứng tỏ điểm ấy giải pháp đều 1 điều xác định.
2. Định lý
a, trọng điểm của con đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
b, nếu một tam giác có một cạnh là 2 lần bán kính của mặt đường tròn nước ngoài tiếp thì tam giác chính là tam giác vuông.
3. Tính chất đối xứng
-Tâm của con đường tròn là trung ương đối xứng của mặt đường tròn đó.
– ngẫu nhiên đường kính làm sao của mặt đường tròn cũng chính là trục đối xứng của đường tròn đó.
4. Các định lý liên quan đến dây cung và mặt đường kính
1, trong những dây cung của một mặt đường tròn, dây cung lớn nhất là con đường kính.
2, trong một con đường tròn, 2 lần bán kính vuông góc với cùng một dây cung thì đi qua trung điểm dây ấy. Ngược lại, 2 lần bán kính đi qua trung điểm của một dây cung( không phải là mặt đường kính) thì vuông góc cùng với dây cung ấy.
B. Bài xích tập từ bỏ luận
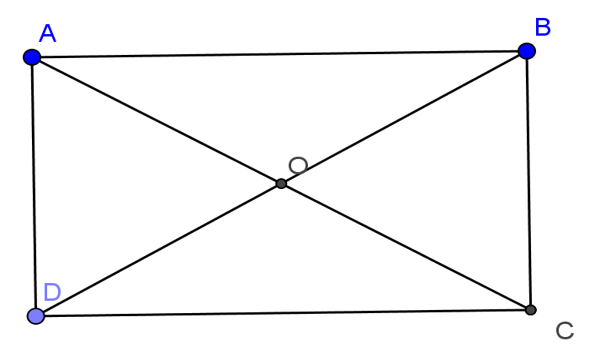
Bài 1: Cho hình chữ nhật ABCD tất cả AD=12cm, CD=16cm. Chứng tỏ rằng 4 điểm A, B, C, D thuộc thuộc một đường tròn. Tính nửa đường kính của mặt đường tròn đó.
Hướng dẫn giải
Gọi O là giao điểm của nhì đường chéo cánh AC cùng BD.
Ta có OA = OB = OC = OD yêu cầu bốn điểm A, B,C,D thuộc thuộc một mặt đường tròn( trung ương O, bán kính OA).
AC2 = AD2 + DC2 = 122 + 162 = 400
=> AC = 20
Bán kính của đường tròn bởi 10cm.
Bài 2: Trong những câu sau, câu nào đúng? Câu làm sao sai?
a, hai tuyến đường tròn phân biệt hoàn toàn có thể có hai điểm chung.
b, hai tuyến đường tròn phân biệt có thể có tía điểm thông thường phân biệt
c, trọng điểm của mặt đường tròn nước ngoài tiếp một tam giác lúc nào cũng phía bên trong tam giác ấy.
Hướng dẫn giải
a. Đúng
b. Sai
c. Đúng
Bài 3: Cho tam giác ABC cân nặng tại A, nội tiếp con đường tròn(O). Đường cao AH giảm đường tròn ngơi nghỉ D.
a, vày sao AD là đường kính của mặt đường tròn (O).
b, Tính số đo góc ACD
c, mang lại BC=24cm,AC=20cm. Tính đường cao AH và nửa đường kính đường tròn (O)
Hướng dẫn giải
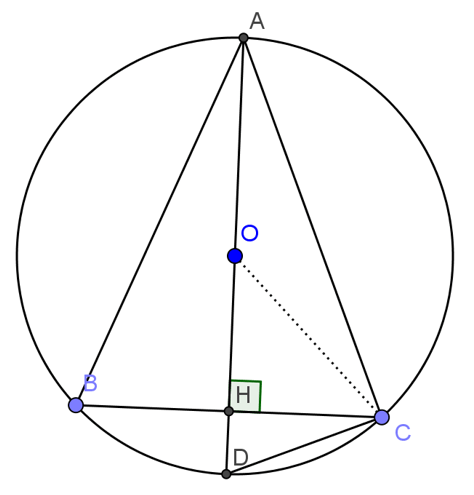
a, Tam giác ABC cân tại A phải AH là con đường trung trực của BC. Cho nên vì thế AD là mặt đường trung trực của BC. Vày O nằm trê tuyến phố trung trực của BC đề nghị O nằm ở AD. Vậy AD là 2 lần bán kính của mặt đường tròn (O).
b, Tam giác ACD nội tiếp mặt đường tròn đường kính AD đề xuất ∠ACD = 90o
c, Ta có bảo hành = HC = BC/2 = 12(cm)
Tam giác AHC vuông trên H buộc phải AH2 = AC2 – HC2 = 202 – 122 = 256
=> AH = 16(cm)
AC2 = AD. AH
AD = AC2/AH = 25(cm)
Bán kính mặt đường tròn(O) bằng 12,5cm.
Bài 4: Cho tam giác ABC, các đường cao bh và CK. Chứng tỏ rằng:
a, tứ điểm B, C, H, K cùng thuộc một đường thẳng.
b, HK HI = một nửa BC (1)
Xét tam giác vuông CBK bao gồm KI là trung tuyến đường ứng với cạnh huyền BC => KI = 1/2 BC (2)
Từ (1) cùng (2) ta suy ra HI=KI=IB=IC. Vậy tư điểm B, K, H, C cùng thuộc con đường tròn trung khu I bán kính IB.
b, Trong đường tròn chổ chính giữa (I) ngơi nghỉ trên, HK là dây, BC là 2 lần bán kính nên KH o
b) MA = R
c) MO = 2R
Hướng dẫn giải
Vì MA cùng MB là những tiếp tuyến đường của mặt đường tròn (O) trên A và B nên: MA ⊥ OA, MB ⊥ OB
Suy ra: ∠MAO = ∠MBO = 90o
a)
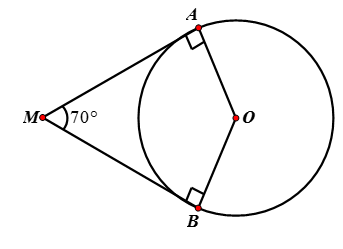
Xét tứ giác MAOB có:
∠AMB + ∠AOB + ∠MAO + ∠MBO = 360o
⇔ ∠AOB = 360o – (∠AMB + ∠MAO + ∠MBO)
= 360o – (70o+ 90o + 90o)
= 110o
Vậy số đo góc ở vai trung phong tạo do hai bán kính OA, OB bởi 110o .
b)
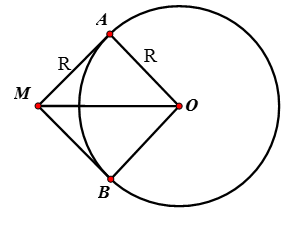
Nếu MA = R
Xét ΔMAO có: MA = AO = R với ∠MAO = 90o
=> Δ MAO vuông cân nặng tại A
=> ang;MOA = 45o
Vậy ∠AOB = 2.∠MOA = 90o
c)
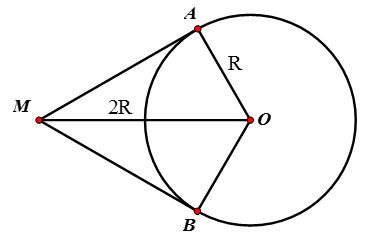
Nếu MO = 2R
Xét ΔMAO vuông trên A có: MO = 2.AO
=> ∠AMO = 30o => ∠AOM = 60o
Vậy: ∠AOB = 2.∠AOM = 120o
Bài 2: Cho con đường tròn (O; R) với dây AB không trải qua O. Bên trên dây AB lấy các điểm M, N làm thế nào để cho AM = MN = NB. Tia OM, ON cắt (O) theo lần lượt tại C và D.
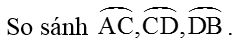
Hướng dẫn giải
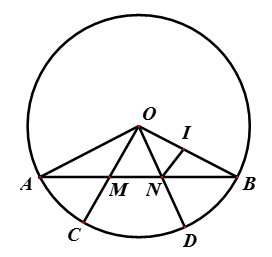
Thât vậy, xét ΔAOM với ΔBON có:
OA = OB = R
∠OAM = ∠OBN (do ΔOAB cân nặng tại O)
AM = BN (gt)
Suy ra ΔAOM = ΔBON(c-g-c)
Suy ra ∠AOM = ∠BON (hai góc tương ứng)
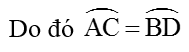
Gọi I là trung điểm của OB. Suy ra NI là mặt đường trung bình của ΔOBM nên NI // OM => ∠MON = ∠ONI(so le trong) (1)
Mặt không giống ta có: OB = OC = R, mà M ∈ OC => OM ∠MAB = ∠ABN (so le trong) (1)
Mặt khác: OA = OB = O’A = O’B phải tứ giác OAO’B là hình thoi, cho nên ∠OAB = ∠ABO’ (2)
Từ (1) với (2) suy ra: ∠MAO = ∠NBO’
Ta có: ΔMOA cân nặng tại O và ΔNO’B cân tại O’ bao gồm góc nghỉ ngơi đáy cân nhau nên ∠MOA = ∠NO’B
Do đó: ΔMOA = ΔNO’B(c.g.c) => AM = BN
Mặt khác hai đường tròn (O) và (O”) bằng nhau nên
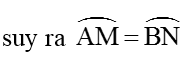
Bài 4: Cho hai tuyến đường tròn (O; R) cùng (O’; R’) giảm nhau tại hai điểm A và B (R o .
Xem thêm: Cung Cấp Chân Tăng Chỉnh Đế Cao Su Cao Cấp, Bền Nhất Hiện Tại
Tương từ bỏ ta có: ∠BAD = 90o
Suy ra: ∠CAD = ∠BAD + ∠BAC = 180o nên 3 điểm C, A, D thẳng hàng.
b) Xét đường tròn (O) có:
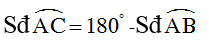
Xét mặt đường tròn (O’) có:
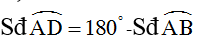
Từ kia suy ra
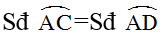
Bài 5: Cho mặt đường tròn (O) đường kính AB. Điểm C thuộc mặt đường tròn (O) thế nào cho SđBC = 30o, điểm M nằm trong cung AC nhỏ. Gọi D cùng E là những điểm đối xứng với M qua AB và OC. Chứng tỏ rằng: ΔDOE đều.
Hướng dẫn giải
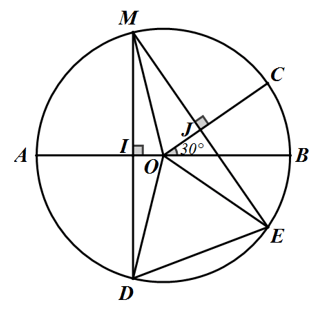
Vì SđBC = 30o => ∠BOC = 30o
Gọi I là giao điểm của MD và AB, J là giao điểm của ME với OC.
Theo mang thiết: M và D đối xứng cùng nhau qua AB, cơ mà M thuộc con đường tròn (O) cần D cũng thuộc con đường tròn (O). Tương tự như E thuộc con đường tròn (O).
Tứ giác MIOJ bao gồm ∠I = ∠J = 90o
=> ∠IMJ + ∠IOJ = 180o
=> ∠IMJ = 180o – ∠IOJ = ∠BOC = 30o
Ta gồm ΔMOD với ΔMOE cân nặng tại O nên:
∠MOD = 180o – 2∠DMO
∠MOE = 180o – 2∠EMO
=> ∠MOD + ∠MOE = 360o – 2(∠DMO + ∠EMO)
⇔ 360o – ∠DOE = 360o – ∠IMJ
⇔ ∠DOE = 2∠IMJ = 60o
Vậy ΔDOE đều.
Bài 6: Cho điểm M hoạt động trên nửa mặt đường tròn (O) đường kính AB. Vẽ hai tiếp đường Ax với By với mặt đường tròn (O). Tiếp con đường tại M với (O) cắt Ax tại C và cắt By tại D; những đường thẳng co và OD cắt (O) thứu tự tại E với F.
a) Tính Sđ EF.
b) tra cứu tập hợp trọng điểm I của con đường tròn nước ngoài tiếp .
Hướng dẫn giải
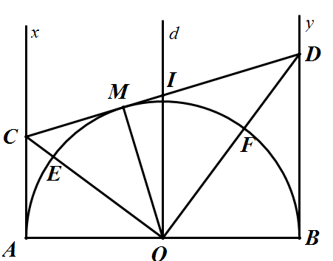
a) do CA cùng BM là nhì tiếp con đường với (O) cần OC là tia phân giác của ∠AOM .
Tương từ bỏ ta có OD là tia phân giác của ∠BOM
Mà ∠AOM với ∠BOM là hai góc kề bù, suy ra OC ⊥ OD
Vậy ta bao gồm ∠COD = 90o hay SđEF = 90o .
b) * Phần thuận:
Vì ΔCOD vuông trên O yêu cầu tâm I của mặt đường tròn nước ngoài tiếp tam giác ΔCOD là trung điểm của CD.
Dễ thấy tứ giác ABCD là hình thang có OI là đường trung bình bắt buộc OI//AC => OI ⊥ AB.
Vậy I hoạt động trên đường thẳng d vuông góc cùng với AB trên O.
* Phần hòn đảo và giới hạn: học sinh tự triệu chứng minh.
Bài 7: Cho AB là dây cung của con đường tròn (O), I là trung điểm của AB. Bên trên cung bé dại AB đem điểm M tùy ý. Gọi giao điểm OI và MI với (O) lần lượt C và N. So sánh và .
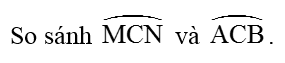
Hướng dẫn giải
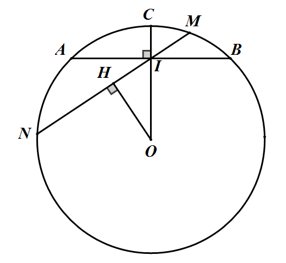
Kẻ OH ⊥ MN
Ta có: ΔOHI vuông trên H cần OH CD. điện thoại tư vấn H và K thứu tự là trung điểm của AB và CD. Chứng minh rằng:
a) MH > MK
b) ∠MOH > ∠MOK
Hướng dẫn giải
a) vì chưng H, K theo lần lượt là trung điểm của AB, CD đề xuất OH ⊥ AB, OK ⊥ CD (quan hệ giữa 2 lần bán kính và dây cung).
Ta có: AB > CD => OH MH > MK
Vì ∠MHO = ∠MKO = 90o nên H, K cùng thuộc con đường tròn đường kính MO.
Trong đường tròn 2 lần bán kính MO, ta tất cả MH > MK
Mặt khác: ∠MOH = 50% SđMH
∠MOK = 1/2 SđMK
Từ đó suy ra: ∠MOH > ∠MOK .
Bài 10: Trên đường tròn (O; R), mang lần lượt theo và một chiều các điểm A, B, C, D sao cho
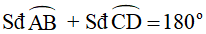
Chứng minh rằng SΔAOB = SΔCOD .
Hướng dẫn giải
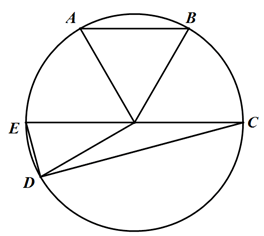
Kéo nhiều năm OC giảm đường tròn (O) trên E.
Do đó: ΔAOB = ΔEOD yêu cầu SΔAOD = SΔEOD (1)
Mặt khác: ΔEOD cùng ΔCOD bao gồm chung độ cao kẻ từ bỏ D xuống EC và độ dài hai lòng EO = OC yêu cầu SΔEOD = SΔCOD (2)
Từ (1) cùng (2) suy ra: SΔAOB = SΔCOD .
Chuyên đề: hình trụ – Hình Nón – Hình Cầu
A. Cách thức giải
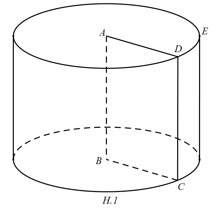
1. Tư tưởng hình trụ
Khi xoay hình chữ nhật ABCD một vòng xoay cạnh AB cố định và thắt chặt ta được một hình trụ (H.1)
– AD cùng BC quét đề nghị hai đáy của hình trụ. HÌnh tròn (A) với (B) đều nhau và phía bên trong hai mặt phẳng song song.
– DC quét yêu cầu mặt bao quanh của hình trụ, DC và EF là hai tuyến phố sinh. Độ dài đường sinh là độ cao của hình trụ.
2. Công thức
(R là nửa đường kính đáy, h là chiều cao, S là diện tích đáy).
C. Bài tập từ luận
Bài 1: Một thứ thể có mẫu mã trụ (H2) nửa đường kính đường tròn lòng và chiều cao của nó đều bằng 2a (cm). Fan ta khoan một lỗ cũng có thể có dạng hình trụ có bán kính đáy với độ sâu đều bằng a (cm).
a) Tính thể tích phần đồ vật thể còn lại.
b) nếu ta tô cả bên trong lẫn phía bên ngoài vật thể thì diện tích vật thể được che phủ là bao nhiêu?
Hướng dẫn giải
a) hotline thể tích những hình trụ lớn, hình trụ bé dại lần lượt là V1, V2
Thể tích đề xuất tìm sẽ là:
V = V1 – V2
V = π(2a)2.2a – π.a2.a
= 8πa3 – πa3
= 7πa3 (cm3)
b) diện tích cần kiếm tìm bằng diện tích s toàn phần của hình trụ to cộng thêm diện tích s xung quanh của hình trụ nhỏ:
S = 2π.2a.2a + 2π.(2a)2+ 2π.a.a
= 8πa2 + 8πa2 + 2πa2
= 18πa2 (cm2)
Bài 2: Có 2 lọ có dạng hình trụ, các size như ở hình 3. Hãy đối chiếu dung tích của 2 lọ và ăn diện tích xung quanh của 2 lọ.
Hướng dẫn giải
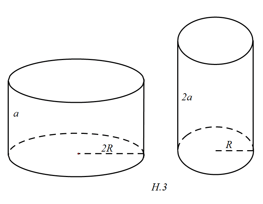
a) V1 = πR2 . 2a = 2πR2a
V2 = π.(2R)2.a = 4πR2a
=>V1 = 2V2
b) S1 = 2πR.2a = 4πR.a
S2 = 2π.2R.a = 4πRa
=> S1 = S2
Bài 3: Cho hình lăng trụ đứng tất cả đáy là lục giác hồ hết cạnh a, chiều cao lăng trụ là h. Xét nhị hình trụ, một hình có đáy là hình tròn nội tiếp đáy lăng trụ, một hình bao gồm đáy là hình tròn ngoại tiếp đáy lăng trụ. độ cao của nhì hình trụ này mọi bằng chiều cao của hình lăng trụ.
a) Tính Sxq của nhì hình trụ đó.
b) Tính tỷ số thể tích, tỷ số Sxq của nhì hình trụ.
Tìm sự liên hệ giữa nhì tỷ số đó.
Hướng dẫn giải
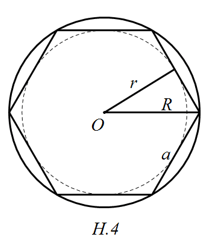
Dễ thấy hình lục giác đều phải sở hữu cạnh a nên:
=> R =a ; r= a√3/2
a) gọi S1, S2 lần lượt là diện tích xung xung quanh của hình tròn ngoại tiếp, nội tiếp hình lăng trụ. Ta có:
S1 = 2πRh = 2πah
S2 = 2πrh = πah√3
b) hotline V1, V2 lần lượt là thể tích của hình tròn trụ ngoại tiếp, nội tiếp hình lăng trụ đó. Ta có:












