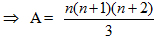CÁC DẠNG TOÁN NÂNG CAO LỚP 7
DẠNG 1: DÃY SỐ MÀ CÁC SỐ HẠNG CÁCH ĐỀU.
Bạn đang xem: Các dạng toán lớp 7 nâng cao
Bài 1: Tính B = 1 + 2 + 3 + ... + 98 + 99Lời giải:Cách 1:B = 1 + (2 + 3 + 4 + ... + 98 + 99).Ta thấy tổng vào ngoặc tất cả 98 số hạng, nếu tạo thành các cặp ta gồm 49 cặp đề nghị tổng kia là:(2 + 99) + (3 + 98) + ... + (51 + 50) = 49.101 = 4949Khi đó B = 1 + 4949 = 4950Lời bình: Tổng B gồm 99 số hạng, ví như ta chia các số hạng đó thành cặp (mỗi cặp gồm 2 số hạng thì được 49 cặp và dư một số hạng, cặp thiết bị 49 thì tất cả 2 số hạng nào? Số hạng dư là bao nhiêu?), mang lại đây học sinh sẽ bị vướng mắc.Ta hoàn toàn có thể tính tổng B theo cách khác như sau:Cách 2:
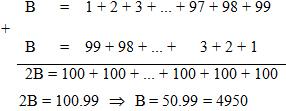
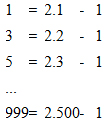
Áp dụng bí quyết 2 của bài xích trên ta có:
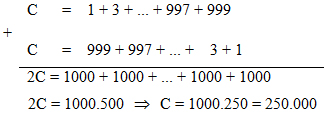
Xem thêm: Tóc Ngắn Mái Thưa Cho Mặt Vuông, Tóc Mái Cho Mặt Vuông
Tính D = 10 + 12 + 14 + ... + 994 + 996 + 998Nhận xét: các số hạng của tổng D đa số là các số chẵn, áp dụng cách có tác dụng của bài xích tập 3 để tìm số những số hạng của tổng D như sau:Ta thấy: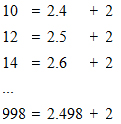
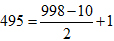
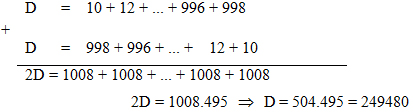
Thực hóa học
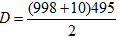
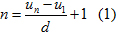
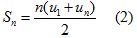
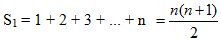
DẠNG 2: DÃY SỐ MÀ CÁC SỐ HẠNG KHÔNG CÁCH ĐỀU.
Bài 1. Tính A = 1.2 + 2.3 + 3.4 + … + n.(n + 1)Lời giải:Cách 1:Ta thấy mỗi số hạng của tổng trên là tích của nhị số tự nhên liên tiếp, khi đó:Gọi a1 = 1.2 → 3a1 = 1.2.3 → 3a1 = 1.2.3 - 0.1.2 a2 = 2.3 → 3a2 = 2.3.3 → 3a2 = 2.3.4 - 1.2.3 a3 = 3.4 → 3a3 = 3.3.4 → 3a3 = 3.4.5 - 2.3.4 ………………….. An-1 = (n - 1)n → 3an-1 =3(n - 1)n → 3an-1 = (n - 1)n(n + 1) - (n - 2)(n - 1)n an = n(n + 1) → 3an = 3n(n + 1) → 3an = n(n + 1)(n + 2) - (n - 1)n(n + 1)Cộng từng vế của những đẳng thức trên ta có:3(a1 + a2 + … + an) = n(n + 1)(n + 2)