BÀI TẬP TAM GIÁC ĐỒNG DẠNG NÂNG CAO

Bộ tài liệu có 16 trang, bao hàm hơn trăng tròn bài tập về chuyên đề tam giác đồng dạng tu dưỡng học sinh xuất sắc lớp 8. Những bài tập giúp các em học sinh có thể phát triển tư duy, đồng thời chuẩn bị cho bản thân một hành trang tốt nhất có thể đối với môn học này. Tài liệu không chỉ giúp các em học tập sinh giỏi ôn thi, mà còn là nguồn tư liệu đặc trưng giúp các em học viên yêu thích môn toán có thể rèn luyện được.

Bạn đang xem: Bài tập tam giác đồng dạng nâng cao

TẢI XUỐNG PDF 

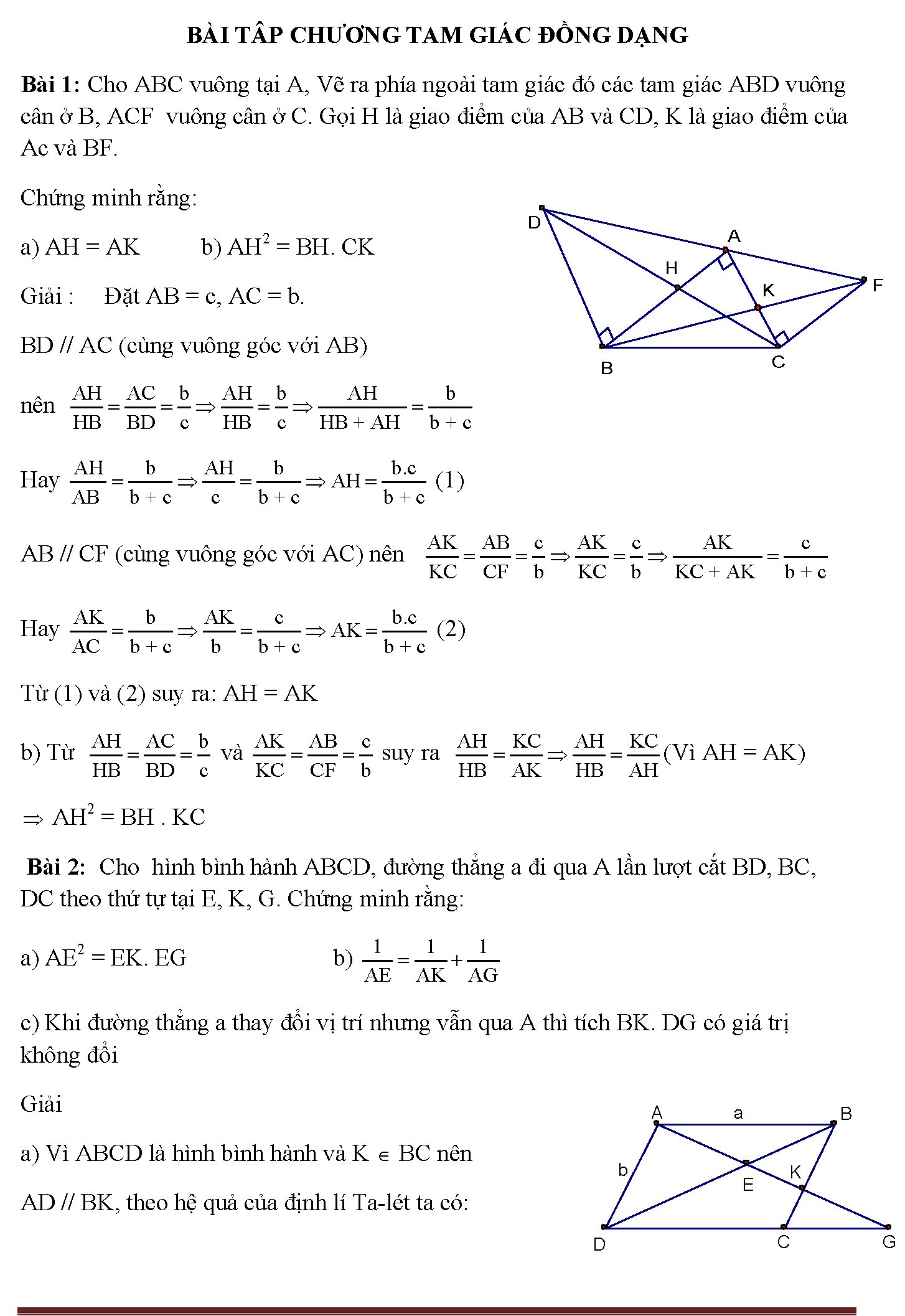
1. BÀI TÂP CHƯƠNG TAM GIÁC ĐỒNG DẠNG bài xích 1: mang đến ABC vuông tại A, Vẽ ra phía quanh đó tam giác đó những tam giác ABD vuông cân nặng ở B, ACF vuông cân nặng ở C. Gọi H là giao điểm của AB cùng CD, K là giao điểm của Ac và BF. Chứng minh rằng: a) AH = AK b) AH2 = BH. Ck Giải : Đặt AB = c, AC = b. BD // AC (cùng vuông góc với AB) buộc phải Hay (1) AB // CF (cùng vuông góc với AC) phải Hay (2) tự (1) cùng (2) suy ra: AH = AK b) Từ và suy ra (Vì AH = AK) AH2 = bh . KC bài bác 2: đến hình bình hành ABCD, con đường thẳng a trải qua A lần lượt cắt BD, BC, DC theo máy tự trên E, K, G. Minh chứng rằng: a) AE2 = EK. EG b) c) Khi đường thẳng a chuyển đổi vị trí tuy vậy vẫn qua A thì tích BK. DG có mức giá trị không đổi Giải a) bởi ABCD là hình bình hành cùng K BC buộc phải AD // BK, theo hệ quả của định lí Ta-lét ta có:

2. B) Ta có: ; cần (đpcm) c) Ta có: (1); (2) Nhân (1) cùng với (2) vế theo vế ta có: không đổi (Vì a = AB; b = AD là độ dài hai cạnh của hình bình hành ABCD ko đổi) bài bác 3: mang lại tứ giác ABCD, các điểm E, F, G, H theo vật dụng tự chia trong các cạnh AB, BC, CD, da theo tỉ số 1:2. Minh chứng rằng: a) EG = FH b) EG vuông góc với FH Giải điện thoại tư vấn M, N theo máy tự là trung điểm của CF, DG Ta bao gồm CM = CF = BC EM // AC (1) Tương tự, ta có: NF // BD (2) mà lại AC = BD (3) trường đoản cú (1), (2), (3) suy ra : EM = NF (a) tương tự như như trên ta có: MG // BD, NH // AC cùng MG = NH = AC (b) còn mặt khác EM // AC; MG // BD và AC BD EM MG (4) Tương tự, ta có: (5) trường đoản cú (4) và (5) suy ra (c) trường đoản cú (a), (b), (c) suy ra EMG = FNH (c.g.c) EG = FH b) call giao điểm của EG và FH là O; của EM với FH là P; của EM và FN là Q thì cơ mà (đối đỉnh), ( EMG = FNH) Suy ra EO OP EG FH

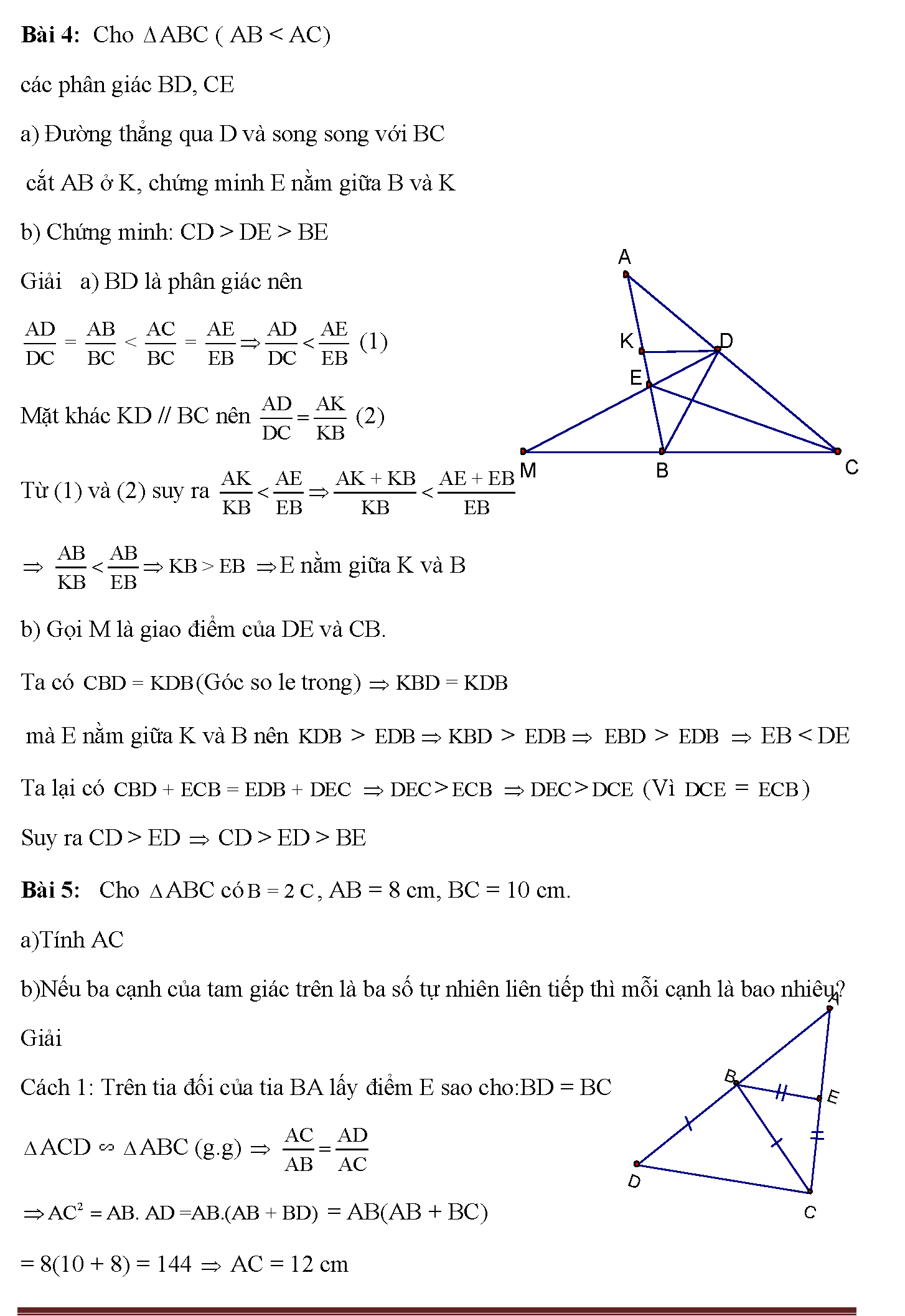
3. Bài xích 4: mang đến ABC ( AB DE > BE Giải a) BD là phân giác buộc phải (1) còn mặt khác KD // BC yêu cầu (2) từ (1) với (2) suy ra E nằm giữa K với B b) điện thoại tư vấn M là giao điểm của DE và CB. Ta bao gồm (Góc so le trong) nhưng E nằm trong lòng K với B buộc phải > > > EB > (Vì = ) Suy ra CD > ED CD > ED > BE bài bác 5: mang lại ABC tất cả , AB = 8 cm, BC = 10 cm. A)Tính AC b)Nếu ba cạnh của tam giác bên trên là bố số từ nhiên thường xuyên thì mỗi cạnh là bao nhiêu? Giải phương pháp 1: bên trên tia đối của tia tía lấy điểm E sao cho:BD = BC ACD ABC (g.g) = AB(AB + BC) = 8(10 + 8) = 144 AC = 12 cm

4. Phương pháp 2: Vẽ tia phân giác BE của ABE ngân hàng á châu acb = 8(8 + 10) = 144 AC = 12 cm b) gọi AC = b, AB = a, BC = c thì tự câu a ta gồm b2 = a(a + c) (1) bởi b > anên có thể b = a + 1 hoặc b = a + 2 + ví như b = a + 1 thì (a + 1)2 = a2 + ac 2a + 1 = ac a(c – 2) = 1 a = 1; b = 2; c = 3(loại) + giả dụ b = a + 2 thì a(c – 4) = 4 – với a = 1 thì c = 8 (loại) – với a = 2 thì c = 6 (loại) – với a = 4 thì c = 6 ; b = 5 Vậy a = 4; b = 5; c = 6 bài bác 6: cho ABC cân nặng tại A và O là trung điểm của BC. Một điểm O di động cầm tay trên AB, rước điểm E trên AC làm thế nào cho . Chứng minh rằng a) DBO OCE b) DOE DBO OCE c) DO, EO lần lượt là phân giác của những góc BDE, CED d) khoảng cách từ O mang đến đoạn ED không thay đổi khi D cầm tay trên AB Giải a) Từ với (gt) DBO OCE b) tự câu a suy ra (1) do B, O ,C trực tiếp hàng đề nghị (2) trong tam giác EOC thì (3) từ bỏ (1), (2), (3) suy ra DOE với DBO gồm (Do DBO OCE) cùng (Do OC = OB) và đề nghị DOE DBO OCE

5. C) tự câu b suy ra vày là phân giác của những góc BDE Củng trường đoản cú câu b suy ra EO là phân giác của những góc CED c) điện thoại tư vấn OH, OI là khoảng cách từ O cho DE, CE thì OH = OI, mà lại O cố định nên OH không đổi OI không thay đổi khi D di động trên AB bài bác 7: mang đến tam giác ABC, trung con đường AM. Qua điểm D trực thuộc cạnh BC, vẽ mặt đường thẳng song song cùng với AM, giảm AB, AC tại E và F a) chứng tỏ DE + DF không đổi khi D cầm tay trên BC b) Qua A vẽ đường thẳng tuy nhiên song cùng với BC, giảm FE tại K. Chứng tỏ rằng K là trung điểm của sắt Giải a) DE // AM (1) DF // AM (2) từ (1) và (2) suy ra DE + DF = = không thay đổi b) AK // BC suy ra FKA AMC (g.g) (3) (2) (Vì centimet = BM) trường đoản cú (1) cùng (2) suy ra FK = EK hay K là trung điểm của FE bài 8: mang đến hình bình hành ABCD tất cả đường chéo cánh lớn AC,tia Dx cắt SC, AB, BC lần lượt tại I, M, N. Vẽ CE vuông góc với AB, CF vuông góc cùng với AD, BG vuông góc với AC. Call K là điểm đối xứng với D qua I. Chứng tỏ rằng a) IM. IN = ID2 b) c) AB. AE + AD. AF = AC2 Giải

6. A) trường đoản cú AD // centimet (1) từ CD // AN (2) từ (1) và (2) suy ra = hay ID2 = IM. IN b) Ta gồm (3) tự ID = IK với ID2 = IM. IN suy ra IK2 = IM. IN (4) tự (3) với (4) suy ra c) Ta gồm AGB AEC AB. AE = AG(AG+CG) (5) CGB AFC (vì CB = AD) AF . AD = AC. CG AF . AD = (AG + CG) .CG (6) cùng (5) và (6) vế theo vế ta có: AB. AE + AF. AD = (AG + CG) .AG + (AG + CG) .CG AB. AE + AF. AD = AG2 +2.AG.CG + CG2 = (AG + CG)2 = AC2 Vậy: AB. AE + AD. AF = AC2 bài bác 9: mang đến tam giác ABC tất cả BC bởi trung bình cùng của AC cùng AB; call I là giao điểm của những phân giác, G là trung tâm của tam giác. Chứng minh: IG // BC Giải Gọi khoảng cách từ a, I, G mang đến BC thứu tự là AH, IK, GD vì I là giao điểm của ba đường phân giác nên khoảng cách từ I đến tía cạnh AB, BC, CA cân nhau và bởi IK. Vị I phía bên trong tam giác ABC nên: SABC = SAIB + SBIC + SCIA BC.AH = IK(AB+BC+CA) (1) cơ mà BC = AB + CA = 2 BC (2) chũm (2) vào (1) ta có: BC. AH = IK. 3BC IK = AH (a) vị G là trung tâm của tam giác ABC nên:

7. SBGC = SABC BC . GD = BC. AH GD = AH (b) từ (a) cùng (b) suy ra IK = GD hay k/ giải pháp từ I, G mang đến BC đều nhau nên IG // BC bài 10: đến điểm M cầm tay trên đáy nhỏ tuổi AB của hình thang ABCD, gọi O là giao điểm của hai ở bên cạnh DA, CB. Gọi G là giao điểm của OA và CM, H là giao điểm của OB và DM. CMR: lúc M di động trên AB thì tổng không đổi Giải Qua O kẻ mặt đường thẳng song với AB cắt CM, DM theo vật dụng tự ngơi nghỉ I với K. Theo định lí Talét ta có: ; (1) Qua M vẽ mặt đường thẳng vuông góc với AB cắt IK, CD theo vật dụng tự ở p và Q, ta có: ko đổi vì FO là khoảng cách từ O cho AB, MQ là mặt đường cao của hình thang đề nghị không thay đổi (2). Tự (1) với (2) suy ra không đổi bài bác 11: mang đến tam giác ABC (AB 8. (P AD); CQ // AG (Q OI) thì = 900 gọi trung điểm của BC là K, ta có BPK = CQK (g.c.g) CQ = BP BPD = CQI (g.c.g) CI = BD (4) cố (4) vào (3) ta tất cả CF = cha (b) từ bỏ (a) cùng (b) suy ra BE = CA bài bác 12: cho tam giác ABC vuông trên A, (AC > AB), mặt đường cao AH. Bên trên tia HC rước D thế nào cho HD = HA. Đường vuông góc với BC tại D cắt AC tại E. M là trung điểm BE. A) chứng minh BEC đồng dạng với ADC. B) Tính số đo góc AHM. Bài 13: đến tứ giác lồi ABCD. Tìm kiếm tập hòa hợp điểm O nằm trong tứ giác thế nào cho hai tứ giác OBCD cùng OBAD có diện tích s bằng nhau. (Không yêu cầu chứng minh phần đảo). 12 a) vày DEC ABC (Hai tam giác vuông tất cả chung) Xét BEC và ADC tất cả chung phối hợp (*) => BEC ADC (g.c.g) b b) BEC ADC => , AHD vuông cân tại H cần M trung điểm BE nên: AM = MB = ME BMA vuông cân nặng tại M AB2 =2BM2 hay cơ mà AB2 = BH.BC (HS đề nghị c/m); BH.BC = BE.BM BHM BEC ADC

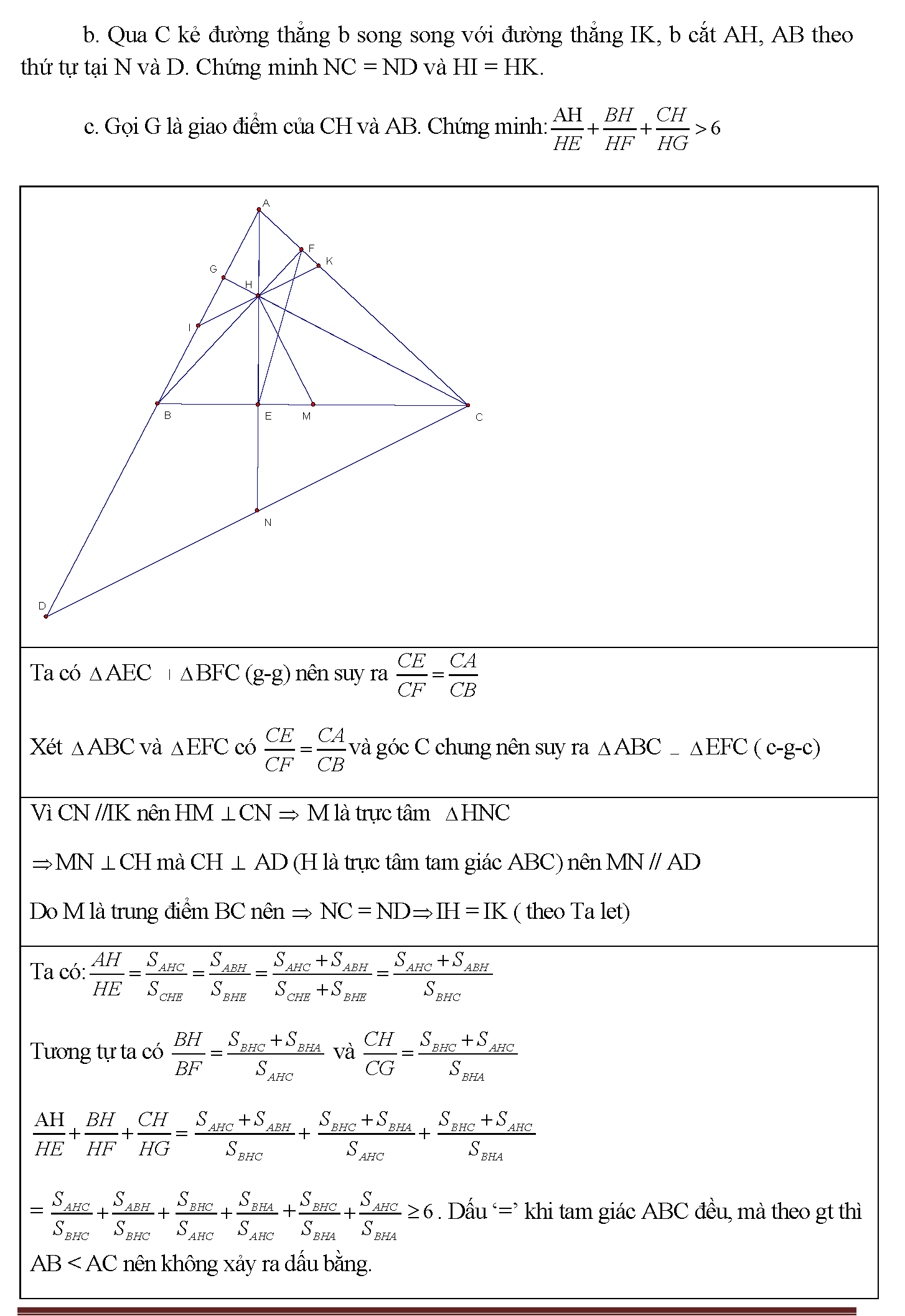
9. B b) BEC ADC => , AHD vuông cân tại H bắt buộc M trung điểm BE nên: AM = MB = ME BMA vuông cân tại M AB2 =2BM2 hay nhưng AB2 = BH.BC (HS phải c/m); BH.BC = BE.BM BHM BEC ADC 13 giả sử O là vấn đề nằm trong tứ giác thỏa mãn: SOBCD =SOBAD. Từ bỏ O kẻ đường thẳng // BC cắt AB tại D1, giảm AC trên B1. Nối OC, OB, AC, BD cùng kẻ những đường cao ha, hb, hc như mẫu vẽ . Khi đó: SOBCD = SBCD+SBOD= SBODA = vày B1D1//BD nên Từ (1) cùng (2) Từ đó HS lập luận suy ra B1D1 trải qua trrung điểm cuả AC. Vậy O vị trí đoạn B1D1¬//BD và trải qua trung điểm AC bài 14. Cho hình vuông vắn ABCD tất cả cạnh bởi a. Hotline E; F;G;H theo thứ tự là trung điểm của các cạnh AB, BC; CD; DA. M là giao điểm của CE và DF. A. Chứng minh: Tứ giác EFGH là hình vuông. B. Chứng minh DF CE cùng MAD cân. C .Tính diện tích MDC theo a.

10. Hội chứng minh: EFGH là hình thoi.

Xem thêm: Chu Chỉ Nhược Của " Ỷ Thiên Đồ Lông Ký 2018 Tung Trailer Võ Thuật Đẹp Mãn Nhãn

Chứng minh có 1 góc vuông. Tóm lại Tứ giác EFGH là hình vuông vắn mà vuông trên C vuông trên M . Giỏi CE DF. điện thoại tư vấn N là giao điểm của AG cùng DF. Chứng minh tương tự: AG DF GN//CM mà lại G là trung điểm DC đề nghị N là trung điểm DM. Trong MAD có AN vừa là đường cao vừa là trung con đường MAD cân nặng tại A. Cho nên vì thế : mà : . Vậy : . Vào theo Pitago ta gồm : . Vì thế : bài bác 15: đến tam giác ABC nhọn (AB11. B. Qua C kẻ con đường thẳng b tuy nhiên song với đường thẳng IK, b cắt AH, AB theo máy tự trên N cùng D. Chứng minh NC = ND với HI = HK. C. điện thoại tư vấn G là giao điểm của CH với AB. Chứng minh: Ta gồm AEC BFC (g-g) đề xuất suy ra Xét ABC cùng EFC gồm và góc C chung cần suy ra ABC EFC ( c-g-c) bởi CN //IK cần HM cn M là trực trọng điểm HNC MN CH mà CH AD (H là trực vai trung phong tam giác ABC) yêu cầu MN // AD do M là trung điểm BC phải NC = ND IH = IK ( theo Ta let) Ta có: giống như ta có và = + . Vết ‘=’ lúc tam giác ABC đều, nhưng mà theo gt thì AB 12. Bài xích 16: Cho hình vuông vắn ABCD. Trên BC rước điểm E, qua A kẻ con đường thẳng vuông góc với AE, mặt đường thẳng này giảm CD tại F. Hotline I là trung điểm của EF, AI cắt CD trên K. Qua E kẻ đường thẳng tuy vậy song cùng với AB, mặt đường thẳng này giảm AI tại G. A. Chứng tỏ AE = AF. B. Chứng minh tứ giác EGFK là hình thoi. C. Chứng tỏ AKF đồng dạng CAF. D. Bên trên cạnh AB đem điểm M sao để cho BE = BM. Tìm địa chỉ của điểm E trên cạnh BC để diện tích s DEM đạt giá trị to nhất? ABE = ADF (cạnh góc vuông, góc nhon) suy ra AE = AF Tam giác AEF vuông cân nặng suy ra AI EF (1) Tứ giác EGFK là hình bình hành (hai đường chéo cánh cắt nhau tại trung điểm từng đường do IEG = IFK) (2) từ (1) với (2) suy ra EGFK là hình thoi Xét AKF và CAF có chung góc F; lại có tam giác EAF vuông cân cần = suy ra nhị tam giác đồng dạng gọi cạnh hình vuông vắn là a . Đặt BE = BM = x suy ra CE = a – x ; AM = a – x = = đạt giá chỉ trị lớn số 1 là lúc x –a = 0 tức x = a nghĩa là lúc đó E trùng C

13. Bài xích 17: vào tam giác ABC, các điểm A, E, F tương xứng nằm trên các cạnh BC, CA, AB sao cho: . A) chứng minh rằng: . B) cho AB = 5, BC = 8, CA = 7. Tính độ nhiều năm đoạn BD. A) Đặt . Ta gồm (*) Qua D, E, F thứu tự kẻ những đường trực tiếp vuông góc cùng với BC, AC, AB cắt nhau tại O. Suy ra O là giao điểm cha đường phân giác của tam giác DEF. (1) Ta bao gồm (2) (1) & (2) (**) (*) và (**) . B) chứng tỏ tương từ bỏ câu a) ta có: , (3) Ta lại sở hữu CD + BD = 8 (4) (3) & (4) BD = 2,5

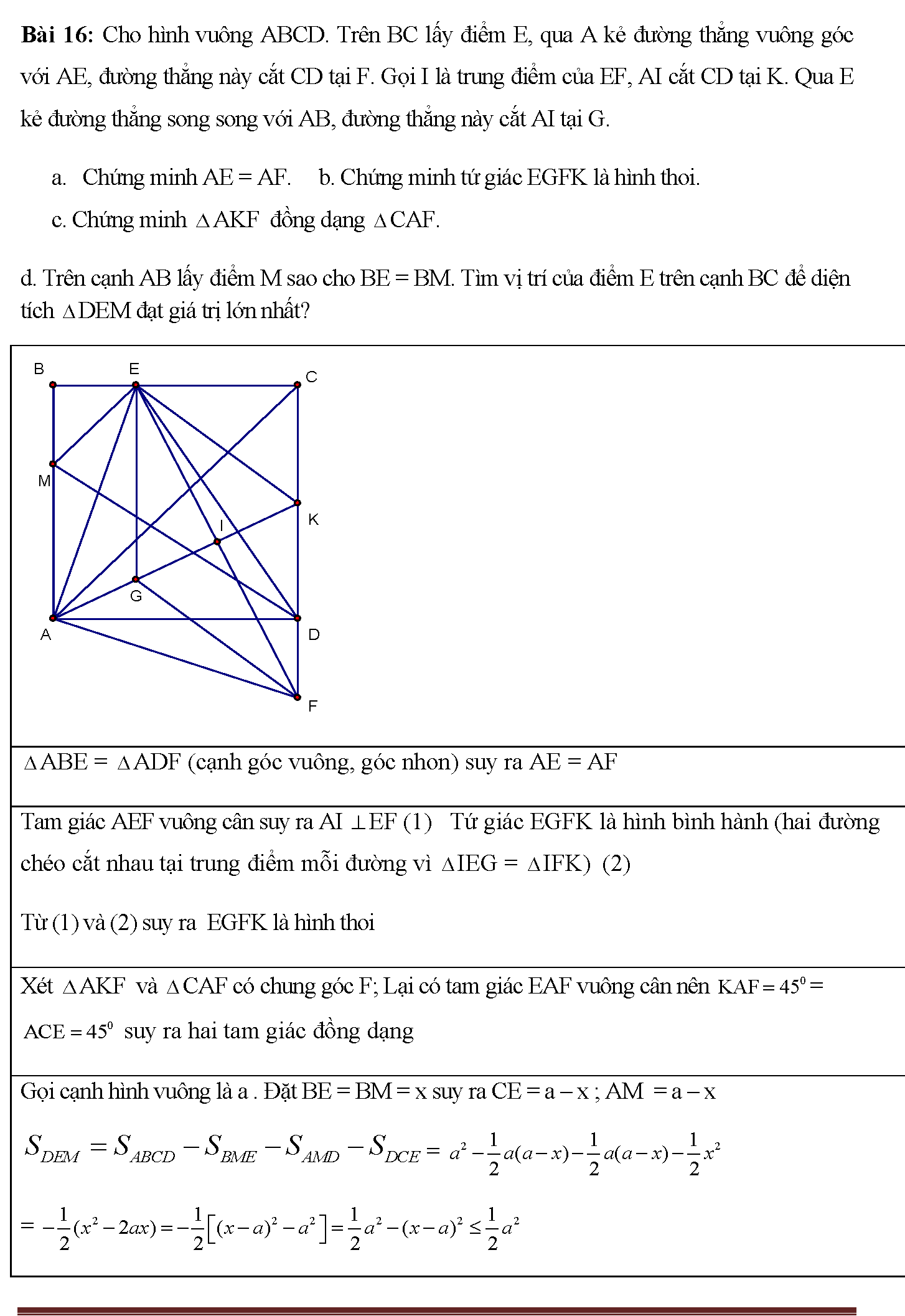
14. Bài bác 18: đến tam giác ABC vuông trên A (AC > AB), đư¬ờng cao AH (H BC). Bên trên tia HC đem điểm D làm sao cho HD = HA. Ьường vuông góc với BC tại D giảm AC trên E. 1. Minh chứng rằng hai tam giác BEC cùng ADC đồng dạng. Tính độ dài đoạn BE theo . 2. Call M là trung điểm của đoạn BE. Chứng tỏ rằng nhì tam giác BHM cùng BEC đồng dạng. Tính số đo của góc AHM 3. Tia AM cắt BC tại G. Chứng minh: . 1 + nhị tam giác ADC với BEC có: Góc C chung. (Hai tam giác vuông CDE và CAB đồng dạng) vị đó, chúng dồng dạng (c.g.c). Suy ra: (vì tam giác AHD vuông cân tại H theo trả thiết). Nên cho nên tam giác ABE vuông cân nặng tại A. Suy ra: 2 Ta có: (do ) nhưng mà (tam giác AHD vuông cân nặng tại H) nên (do ) cho nên vì thế (c.g.c), suy ra: 3 Tam giác ABE vuông cân nặng tại A, đề xuất tia AM còn là một phân giác góc BAC. Suy ra: , mà vày đó: bài bác 19: Cho hình vuông vắn ABCD cạnh bằng a. Điểm E trực thuộc cạnh BC, điểm F trực thuộc cạnh AD làm sao cho CE = AF. Các đường trực tiếp AE, BF cắt đường trực tiếp CD theo trang bị tự tại M và N.

15. A.Chứng minh rằng: DN.CM = a2 b. Hotline K là giao điểm của NA với MB. Bác bỏ minh rằng MKN = 900 c. Các điểm E, F gồm vị trí ra sao thì MN bao gồm độ dài bé dại nhất? khi ấy hãy tính diện tích s của tam giác KMN theo a? a K A B F E N D C M từ bỏ gt AB // MN phải ta có: CM.DN = AB2 = a2. B Theo chứng tỏ trên: nên ( vì tía = CB) với ADN = MCB ( = 900) đồng dạng cùng với MBC = & Mà MBC + BMC = 900 và + MBC = 900 Vậy MKN = 900 c vày MN = ND + CD + CM yêu cầu MN bé dại nhất ND + CM nhỏ tuổi nhất (Vì DC ko đổi) Áp dụng bất đẳng thức cosi ta có: ND + cm Dấu “ =” sảy ra khi centimet = doanh nghiệp = a DF và CE thứu tự là mặt đường trung bình của tam giác NBC với tam giác MAD. Hay E,F là trung điểm của BC và AD Vậy MN đạt GTNN bằng 3a lúc E,F là trung điểm của BC với AD. Khí đó SKMN = SKAB + SNAD + SCBM + SABCD = SKAB + 2SABCD. Lại vị tam giác KAB vuông cân nặng tại K bắt buộc đường cao ứng với cạnh AB có độ dài bởi Và SABCD = a2. Vậy SKMN =

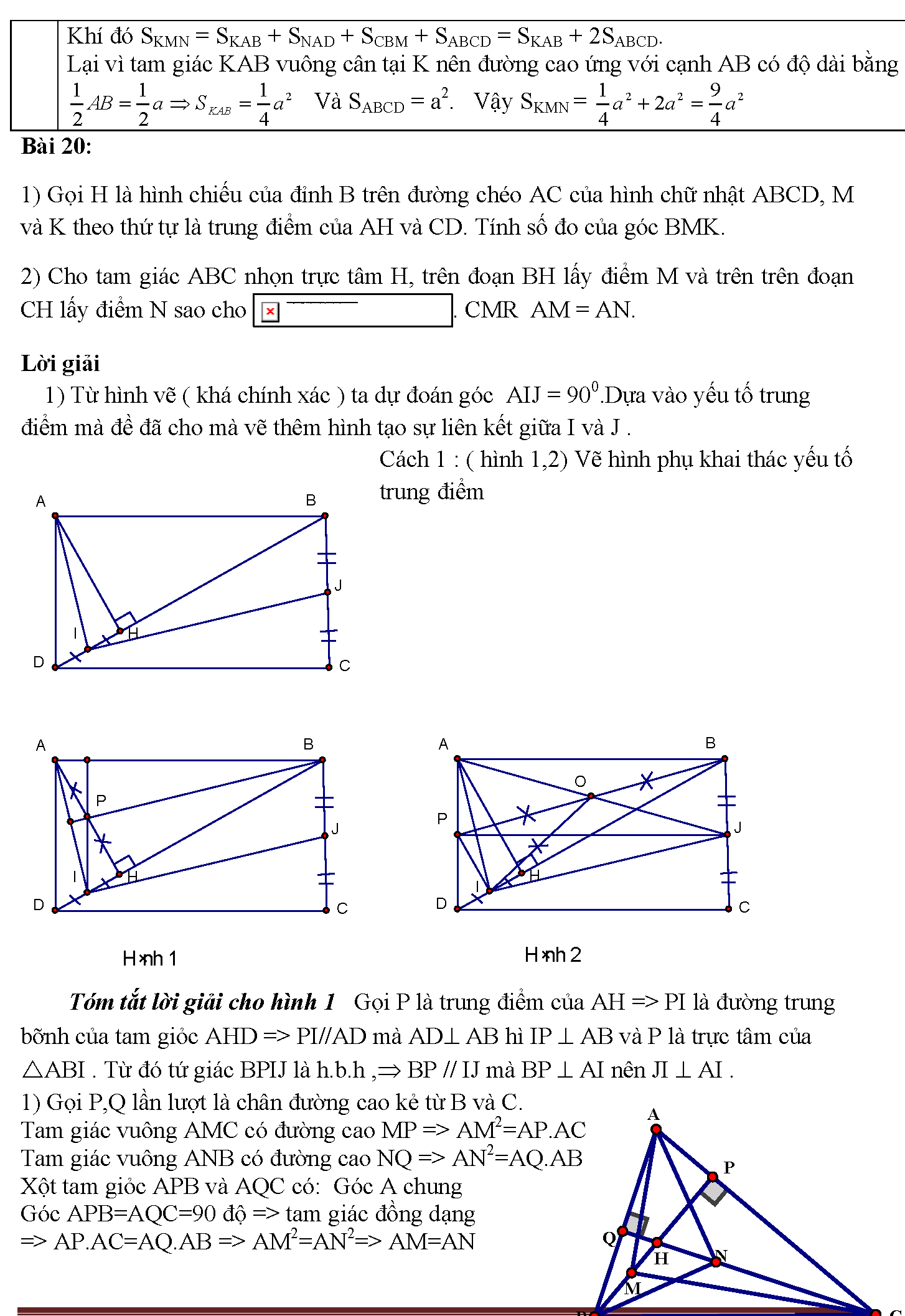
16. Bài bác 20: 1) call H là hình chiếu của đỉnh B bên trên đường chéo AC của hình chữ nhật ABCD, M cùng K theo lắp thêm tự là trung điểm của AH và CD. Tính số đo của góc BMK. 2) đến tam giác ABC nhọn trực trọng điểm H, trên đoạn bảo hành lấy điểm M cùng trên trên đoạn CH rước điểm N sao để cho . CMR AM = AN. Giải thuật 1) Từ hình mẫu vẽ ( khá đúng chuẩn ) ta dự đoán góc AIJ = 900.Dựa vào nhân tố trung điểm nhưng mà đề đã cho mà vẽ thêm hình chế tạo ra sự liên kết giữa I với J . Phương pháp 1 : ( hình 1,2) Vẽ hình phụ khai quật yếu tố trung điểm tóm tắt lời giải cho hình 1 Gọi phường là trung điểm của AH => PI là con đường trung bỡnh của tam giỏc AHD => PI//AD nhưng AD AB hì IP  AB và p là trực trọng tâm của ABI . Từ kia tứ giác BPIJ là h.b.h , BP // IJ mà BP  AI nên JI  AI . 1) hotline P,Q theo thứ tự là chân con đường cao kẻ từ B cùng C. Tam giác vuông AMC tất cả đường cao MP => AM2=AP.AC Tam giác vuông ANB tất cả đường cao NQ => AN2=AQ.AB Xột tam giỏc APB với AQC có: Góc A phổ biến Góc APB=AQC=90 độ => tam giác đồng dạng => AP.AC=AQ.AB => AM2=AN2=> AM=AN

Từ khóa:

chuyên đề tam giác đồng dạng (file word)chuyên đề tam giác đồng dạng toán 8chuyên đề tam giác đồng dạngbài tập tam giác đồng dạng nâng cao có đáp ánchuyên đề tam giác đồng dạng nâng caotam giác đồng dạng lớp 8chuyên đề định lý talet và tam giác đồng dạng lớp 8hai tam giác đồng dạng lớp 8